根据上海、广州、北京等地盾构隧道施工监测资料来看,当衬砌环脱出盾尾后,管片上浮是盾构隧道施工过程中普遍存在的问题。监测资料显示,直径为 6 m 左右的盾构隧道管片上浮一般在 0~60 mm 之间,但有些隧道局部地段上浮超过了100 mm,并引起了衬砌结构侵入建筑限界。对于管片上浮的原因,一些现场工程师和研究人员进行了分析,有些认为同步注浆不充分、管片顶部存在的空隙是导致管片上浮的原因之一,但有些却通过现场监测得出“管片脱出盾尾后的上浮量随着注浆量的增加而增加,反之,上浮量则减少,并出现下沉现象” 。也有的认为,管片上浮是因为覆土较浅或隧道处于软土地层所致,但很多情况下在硬岩地层中的盾构隧道以及覆土较大的隧道也出现了管片上浮现象。这些分析结论并不能全面地解释管片上浮现象的规律,有些观点甚至是相互矛盾的,没有揭露出管片上浮原因的本质。
近些年来,随着越江隧道工程中大直径盾构隧道的应用,施工过程中管片上浮问题表现得更为突出,因此有必要对管片上浮原因深入地研究,找出解决这一问题的对策。本文结合拟建的某大直径盾构隧道工程,采用有限元法对盾构施工过程进行模拟分析,并对地层性质、覆土厚度、注浆材料等因素对管片上浮的影响关系进行分析,从而揭示管片上浮的根本原因,可为制定控制管片上浮的措施提供参考和依据。
2 管片上浮原因分析
2.1 衬砌环受力分析
2.1.1 衬砌成环时受力状态
当衬砌管片刚拼装成环后,衬砌环处于盾尾保护之内,仅受自重作用,其整体运动受盾构机支配。当盾构机掘削土体同时自重作用于地层后,由于一般盾构机重量小于开挖土体的重量,故地层应力会进行重分布,使盾构机在地层作用下略有上浮。这种上浮是一种平均效果,由于盾构机重量沿纵向分布不均匀,所以在软土地层中较重的刀盘部分一般会下沉,而盾尾部分则表现为上扬,即出现“磕头”现象。
2.1.2 衬砌环脱出盾尾时受力状态
(1)软弱土层中的隧道
衬砌环刚脱出盾尾时,衬砌环管片在同步注浆材料的包裹下置于地层中,不计土的拱效应,拱顶压力 p 1 = γ h( γ 为土重度;h 为覆土厚度),隧底压力 p 2 = (h+2R) γ (R 为隧道半径)。假定土压力沿深度方向均匀分布,此时结构受力模式如图 1 所示。
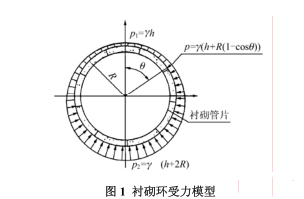
根据图 1 的受力模式,通过计算可知,衬砌结构受到的竖直方向土压力的合力FE 为
根据一般设计,衬砌管片厚度 t 与隧道半径 R的比值近似为一常数,假定取值为 R /10,则管片的重量为
式中: t 为管片厚度;hγ 为混凝土的重度,取 25kN/m 3 ; γ 为土的重度,取 18 kN/m 3 。
将混凝土和土的重度代入式(1)、(2),则可得
一般情况下( t 与 R 的比值为定值),衬砌环刚刚脱出盾尾时,受到的地层向上作用的合力大于衬砌环自重,且二者的比值与隧道直径无关。
(2)岩层中的隧道
当盾构隧道处于地层自稳能力很强的地层(如岩层)中时,管片脱出盾尾后开挖轮廓自身稳定,故衬砌环不受围岩压力作用,在地下水丰富时仅受水的压力作用,根据式(3)可知,处于水中的衬砌环受到的浮力FW 与自重 G 的比值为
同步注浆未凝固时,由于浆液的重度一般大于水的重度,故浆液产生的浮力与自重的比值大于2.4。通过上述计算可知,水或注浆压力的浮力均大于衬砌环自重。
2.2 管片上浮原因
根据力学原理可知,衬砌环脱出盾尾时的衬砌环受力处于不平衡状态,衬砌环有发生运动的趋势。
对软弱地层中的隧道,衬砌环脱出盾尾时受到地层作用,当地层向上作用力的合力与衬砌自重的差值大于地层对衬砌环的摩擦力时,衬砌环将发生上浮。衬砌环上浮的结果引起地层应力的再次重分布,表现为隧底地层因应力释放而产生向上的位移,同时隧道顶部地层应力增加,上方覆土也随之隆起。随着地层应力的调整,衬砌环受到的竖向合力 F 逐渐减小,最终衬砌结构和地层达到了新的平衡而停止运动,可见软弱地层中管片上浮的发生是施工过程中地层应力重分布的结果。由于在土质地层中,地层应力释放、调整的过程较为缓慢,所以盾构管片的上浮从脱出盾尾开始,持续较长一段时间才会结束。
对于围岩能够自稳的隧道,衬砌环脱出盾尾后不受地层压力作用,如果没有水或未凝浆液的作用,一般不会发生上浮。当处于富水地层或采用惰性浆液同步注浆时,衬砌环将会发生较大的上浮,且持续时间相对较短。
超挖、推力不均衡、纠偏、注浆压力不均衡等因素对管片位移可能有影响,但其引起管片位移的方向(可能向下)有偶然性,因此不可能是管片发生规律性上浮的本质原因。
为了验证上述分析所得出规律的合理性,下面通过有限元法对施工过程进行模拟计算,考察软弱地层中盾构管片的位移规律。
3 施工过程模拟计算
3.1 计算方法
本文采用有限元法对施工过程进行模拟计算。由弹性力学理论可知,模拟计算中加载顺序对地层应力场无影响,但对地层位移场有影响,所以在分析计算中,应该按照实际的施工过程来模拟计算。
计算中,将相对完整的施工阶段作为一个施工步,并设每个施工步包含若干增量步,则与该施工步相应地开挖释放荷载可在所包含的增量步中逐步释放,从而真实地模拟施工过程。对各施工阶段的状态,有限元分析的一般表达式为
式中: L 为施工步总数;[ K ] i 为第 i 施工步岩土体和结构的总刚度矩阵;[ K ] 0 为岩土体和结构(施工开始前存在)的初始总刚度矩阵; [ΔK] λ为施工中第λ 施工步的岩土体和结构刚度的增量或减量; {ΔFr }i为第 i 施工步开挖边界上的释放荷载的等效节点力; {ΔFg }i为第 i 施工步新增自重的等效节点力;{ΔFp } i为第 i 施工步增量荷载的等效节点力; { pδ} i 为第 i 施工步的结点位移增量。
对每个施工步,增量加载过程的有限元分析表达式为
式中: M 为各施工步增量加载的次数; [K ] ij 为第 i施工步中施加第 j 荷载增量步时的刚度矩阵; {Δδ} ij 为第 i 施工步第 j 增量步的节点位移增量;αij 为与第 i 施工步第 j 增量步相应的开挖边界释放荷载系数; {ΔFg}ij 为第 i 施工步第 j 增量步新增单元自重等效节点力; {ΔFp}ij 为第 i 施工步第 j 增量步增量荷载的等效节点力。
根据盾构隧道施工过程,计算步骤为
①始地应力场计算;
②盾构掘进,切削土体,释放部分应力;
③盾构机荷载作用,应力重分布;
④衬砌环脱出盾尾与同步注浆共同承受地层荷载。
3.2 基本参数
结合拟建的某越江隧道的设计情况,隧道内径为 13.7 m ,外径为 15.0 m 。盾构机参数如下:盾构机外径为 15.4 m ;盾构机内径为 15.2 m ;盾构机总重量为 3 200 t ,平均重度为 12.27 kN/m 3 。
管片材料为 C60 钢筋混凝土,隧道所处地层为粉质黏土,同步注浆采用惰性浆液。各材料的物理、力学特征参数见表 1 。
3.3计算模型
计算模型如图 2 所示,其中衬砌结构采用梁单元,土体以及注浆材料均采用实体单元,且服从德鲁克 - 普拉格( D-P )屈服准则。
3.4计算结果及分析
按照上述方法,取覆土厚 12.0 m 计算。得到各施工阶段相对上一阶段的位移变化值如图 3 所示。从图 3 的地层位移变化可以看出,盾构机掘进过程中,由于施工对地层的扰动引起部分荷载释放,造成周边地层应力释放,土体向隧道内位移;当盾构机自重荷载作用于地层上后,由于盾构机平均重度(12.3 kN/m 3 ) 小于地层重度( 18.5 kN/m 3 ),故在地层应力差的作用下盾构略有上浮。当衬砌环脱出盾尾与同步注浆材料共同承受地层荷载后,由于衬砌环的平均重度仅仅为 4.3 kN/m 3 ,故衬砌环产生上浮,隧底管片向上位移 59 mm ,拱顶管片上移 26 mm ,管片呈 “ 横鸭蛋 ” 形,平均整体上浮 43 mm 。
通过以上计算结果分析可知,有限元法计算得到的管片位移规律与前面对软弱地层中衬砌环受力及位移原因分析的结论相符。为了进一步研究管片上浮的规律,下面通过对比计算,对衬砌管片上浮的影响因素进行分析。
4 管片上浮影响因素分析
4.1 覆土厚度
在其他条件不变的情况下分别取覆土厚度 h 为8 、 10 、 12 、 15 、 20 m 和 30 m 共 6 种工况进行计算。根据计算结果,相对覆土厚度 h / D ( D 为隧道外径)对地表位移和隧道位移的影响如图 4 所示。从图可知,随着覆土厚度的增加,地表隆起和隧道的向上位移均逐渐下降。
4.2 地层性质
为了考察隧道所处地层的物理力学性质对管片上浮的影响,分别取表 2 所列的几种典型地层进行计算。图 5 为地层类型与隧道位移的关系。从图中可以看出,地层性质对管片位移有较大影响;土质地层中土体强度越高,管片上浮越小,因此软黏土地层中管片上浮最大。
4.3 注浆材料性质
盾壳与衬砌管片外侧之间的空隙在施工中通过同步注浆来填充,对于本工程,盾壳外径为 15.4 m ,管片外径为 15.0 m ,故注浆层的厚度为 0.2 m 。下面对粉质黏土地层条件下不同类型注浆材料对管片上浮的影响分别进行计算,注浆材料性质见表 3 。由于浆液早期强度越高,地层应力释放越少,计算中通过荷载释放系数取值的不同来表现这种差别。
通过同步注浆材料和隧道上浮的影响关系可以看出,采用强度很低的惰性浆液,管片位移明显减小;采用瞬凝浆液和硬性浆液时,管片位移较大,可塑浆液引起的位移居中。
上述现象的原因在于:当注浆材料的强度较低时,在衬砌环和地层应力调整过程中注浆层起到缓冲作用,即当隧道底部的地层应力释放发生向上的位移 Δ 1 时,注浆材料通过自己的体积压缩和流动发生变形 Δ t = t 1 - t 2 ,则隧道的向上位移 Δ = Δ 1 - Δ t ,即管片上浮减少如图 7 所示。相反,当注浆层强度较高时,注浆层自身的变形能力差、缓冲作用下降,即Δ t 减小,所以隧道向上位移 Δ 增大,因此隧道向上位移随着注浆层强度的增大而增大。基于同样原因,当注浆量不饱满时,由于衬砌环和地层之间存在空隙,相当于 Δ t 增大,故隧道位移值减小,所以会出现文献中提到的管片上浮随着注浆量增大而增大的情况。
此外,浆液早期强度出现的时间越晚,地层应力释放越多,作用于衬砌环上的竖向合力越小,引起的衬砌环向上位移也越小,所以在土质地层中采用同样强度的瞬凝性浆液时,管片位移大于采用硬性浆液时的位移。但对于富水基岩地层条件下,引起管片上浮的主要原因是水浮力的作用,故采用瞬凝浆液同步注浆,或通过 2 次注浆及时填充衬砌外侧与开挖轮廓之间的空隙,有效减小管片位移。
5 结 论
根据以上分析可以得出如下主要结论:
(1 )软弱地层中管片上浮的发生是施工过程中地层应力重分布的结果,故上浮过程较为缓慢;围岩能够自稳的隧道中,隧道上浮是水及同步注浆浆液产生的浮力直接作用的结果,上浮过程较为短暂。
(2 )软弱地层中,地层性质、覆土厚度、注浆材料性质等均对管片上浮有影响。
(3 )隧道向上位移随着相对覆土厚度的增大而减小。
(4 )在软土地层中,采用早期强度低,流动性大的注浆材料有利于减小施工期管片上浮(但要注意施工期管片上浮和后期沉降之间的矛盾)、在岩质地层中采用瞬凝型浆液可以减少管片上浮。




