依据盾构工法的特性，拼装好的衬砌脱离盾尾后，由于盾壳原来占据的空间、为衬砌的拼装操作所留空隙、盾构推进时带走的部分黏附于盾壳上的土体所形成的空隙等，在衬砌环背面与实际开挖洞壁间存在环形空隙，使土体暂时处于无支护状态，该空隙即为盾尾间隙。盾尾间隙的大小是由盾构钢壳的厚度和盾尾操作空间决定的，一般在 8～16 cm左右。该间隙若不能及时有效填充，隧道周围土体应力将会逐渐释放，或者造成地下水、泥浆等液体在该间隙环中集聚。依据周围土体本身地质条件的不同，会产生严重后果，如上覆土的下沉、隧道的局部或整体上浮。所以，盾构工法施工中，对盾尾间隙的处理，即壁后注浆是施工的关键。
　　壁后注浆在填充建筑间隙、加固土体的同时，对管片也产生了一定压力，该压力达到一定程度时，可能引起管片局部或整体上浮、错台、开裂、压碎或其他形式的破坏。
　　针对盾构隧道盾尾间隙和壁后注浆的研究方法主要有：理论分析、现场实测、模型试验及数值计算等。Yukinori  等进行了大量盾构隧道壁后注浆的物理模型试验，其研究表明：土的密实度和注浆压力能够显著影响土压力的分布和大小；Ezzeldine 用有限元程序 PISA 模拟了盾构推进、拼装衬砌及壁后注浆对地基变形的影响；国际隧道协会工作报告  中推荐的在管片结构计算时考虑的注浆压力分布模式为三角形分布；张云 在分析盾构法隧道引起地表变形原因的基础上，将盾尾间隙的大小、注浆充填程度、隧道壁面土体受扰动的程度和范围等因素，概化为一均质、等厚的等代层，进而分析了地表变形对等代层参数的敏感性；黄宏伟 等利用探地雷达方法，对上海某盾构隧道盾尾壁后注浆分布进行探测，并进行了初步的分析，对隧道壁后浆液分布情况进行了诊断尝试；Bezuijen  等对一个9.5 m 直径的盾构隧道的两环进行了现场壁后注浆的测试研究，其结果表明：注浆过程中，注浆压力起主导作用，当开挖停止时，注浆浆液的浮力开始产生影响；邓宗伟  等运用 FLAC 3D 2.0，结合盾构隧道壁后注浆的受力特点进行二次开发，对盾构隧道壁后注浆的作用机制进行了研究，探讨了壁后注浆对支护结构和围岩的受力、变形影响的规律；梁精华  针对南水北调中线穿黄隧道盾构法施工中的细砂地层，进行了注浆材料的优化配比试验，并研制了浆体收缩试验装置和大型浆体压力消散试验模型，对注浆后浆体在压力作用下的变形特性进行了试验研究。
　　本文在借鉴已有研究的基础上，采用理论分析的方法，基于柱形扩散理论，在假定壁后注浆呈圆柱形扩散方式的基础上，通过引入等效孔隙率替代土体本身的孔隙率，即将管片脱离盾尾后形成的建筑间隙折算为土体本身的孔隙率，来考虑建筑间隙的影响，对盾构隧道壁后注浆的渗透范围及因注浆而对管片造成的注浆压力进行了理论推导，得到浆液扩散范围及对管片压力的计算式，并通过实例分析，讨论了浆液扩散半径及对管片产生的压力与注浆压力、注浆时间等因素的关系。
2 壁后注浆工艺概述
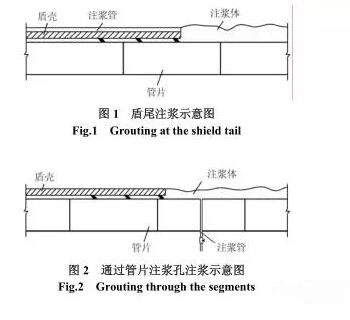
　　依据注浆部位，盾构隧道壁后注浆有两种类型，即盾尾注浆（通过安装在盾构机盾壳上的注浆管注浆，见图 1）和管片注浆（通过管片上的注浆孔注浆，见图 2），两种注浆方式的优缺点比较如表1 所示。

3 浆液扩散模式及计算分析
　　浆液的扩散方式通常有充填注浆、渗透注浆、压密注浆及劈裂注浆等。浆液扩散是一复杂过程，与周围土质、施工工艺、浆液性质、注浆压力、地下水等多种因素有关，各种扩散方式并无明显界线，而且相互包容、相互参杂、相互转化。如在充填注浆过程中存在渗透现象，在渗透注浆过程中存在劈裂现象，在劈裂注浆过程中存在渗透流动，在压密注浆过程中存在劈裂或渗透流动等。
　　本文将盾构隧道壁后注浆的浆液扩散方式考虑为渗透注浆，并将浆液考虑为较为简单的牛顿流体，基于柱形扩散理论进行分析。
3.1 基本假设
　　（1）浆液为牛顿流体
　　假设注浆浆液的流变曲线是通过原点的直线，其方程表达式为

τ=μγ

　　式中： τ 为剪切应力(Pa)； μ 为动力黏度或黏度系数(Pa · s)； γ 为剪切速率(s -1)。大部分单相的均匀体系属牛顿流体，水、大多数化学浆液以及较稀的水泥浆液属牛顿流体 。
　　（2）在一定厚度内浆液沿柱面均匀扩散
　　依据盾构工法特性，盾尾间隙的存在，注浆的主要目的为及时充填盾尾间隙。参考文献[10]中的注浆效果阐述，假设注浆浆液在盾尾间隙影响厚度范围内，沿与隧道管片表面平行的方向均匀扩散。盾尾间隙的厚度影响范围可依据在注浆计算和施工中，实际注浆量与理论注浆量之比值（即注入率）乘以盾尾间隙的厚度来确定。
　　事实上，管片脱离盾尾后，因盾尾间隙造成周围土体一定范围内应力松弛，从而发生向管片外壁方向的位移，造成一定范围内的土体孔隙率远大于原始孔隙率，进而大大提高其渗透系数。基于此，本文假设浆液只在该厚度范围内渗透扩散。
3.2 理论推导
3.2.1 盾尾注浆
　　盾尾注浆时，浆液的渗透扩散模型如图 3 所示，图中Pg 为注浆压力； Pw 为注浆点处的地下水压力；r0 为注浆孔半径；r 为经过注浆时间 t 后浆液的扩散半径；D 为浆液扩散体的厚度，即注浆浆液的影响厚度，依据基本假设，取 D =d λ  ； λ 为注入率；d 为盾尾间隙厚度。

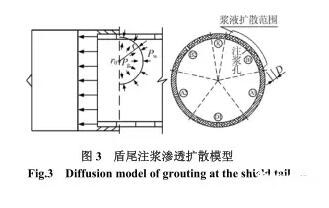
　　此时，浆液扩散厚度范围内的等效孔隙率为

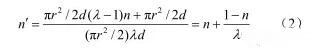
　　式中：n 为土体的原始孔隙率。根据 H. Darcy 定律：

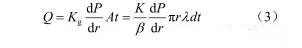
　　式中：K g为浆液在扩散厚度范围内土体中的渗透系数， K g= K/ β  ；K 为浆液扩散厚度范围内土体的渗透系数； β 为浆液黏度与水的黏度比（20℃时水的黏度为 1.010×10 -3 Pa · s），即β =μg/ μw  ；A 为浆液渗透过程中经过的任意半圆柱面面积， A=πr λd  ；t 为注浆时间。
　　根据边界条件，在r0处，浆液压力为Pg ；当浆液扩散半径达到 r 时，浆液压力为Pw 。因而有：

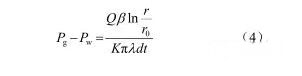
　　因为 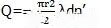为注浆量，并考虑到式（2），记Pg−Pw=ΔP ，于是，有：

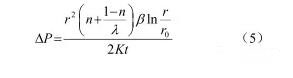
　　故而，任意半径 r 处的注浆压力为

　　则由注浆浆液对管片产生的压力为

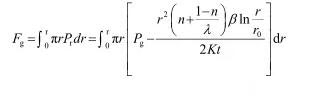
　　解得

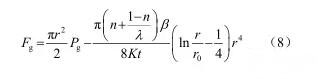
3.2.2 管片注浆
　　经分析可知，采用盾尾注浆时，因注浆孔就在盾构壳体上，盾壳消解了部分注浆压力，在一定程度上阻止了浆液的扩散。采用管片注浆时，注浆孔与盾尾有一定距离，浆液扩散范围会更大，但此范围要受到该距离的影响。
　　浆液的渗透扩散模型如图 4 所示。本模型的隐含假设条件为：在通过管片注浆孔进行管片注浆时，该注浆孔距离盾尾有一定距离，从而能进行完整的圆柱面扩散，实际中会因为注浆孔与盾尾距离较近，使得扩散的柱面并不一定是完整的圆柱面。

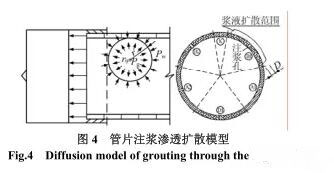
　　经过类似于 3.2.1 节中的推导，可得到与式（5）相同的浆液扩散半径与注浆压力间关系的表达式。但此时的注浆压力对管片产生压力的表达式为

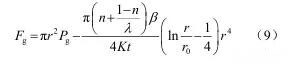
　　比较式（9）与式（8），可见采用管片注浆时，对管片产生的注浆压力是采用盾尾注浆时的 2 倍（实际上，依据盾尾与注浆孔的间距情况，其倍数应该在 1～2 倍之间）。
4 实例分析
　　由浆液扩散半径计算式（5），及对管片产生的压力计算式（8）、式（9）可以看出：壁后注浆浆液的扩散半径及对管片产生的压力大小与注浆压力、注浆时间、浆液黏度、土体孔隙率、土体渗透系数、建筑间隙厚度、注浆管半径等众多因素有关。渗透系数为浆液扩散范围 D 内的渗透系数，盾尾间隙的存在加大了浆液扩散范围的孔隙率，同时大大加大了该部分土体的渗透系数。
　　现假定注浆管半径r0 = 2.5 cm，原土体孔隙率n= 20 %，原土体的渗透系数K 0= 5×10 −4 cm ·s − 1，浆液黏度与水的黏度比 β = 4，取建筑间隙厚度 d =10 cm，注入率 λ = 1.5，注浆点处的地下水压力为Pw = 0。
　　由式（2）可得， n′= 73.33 %，参考考虑土体孔隙比 e 的渗透系数经验公式：

K=2 d2 10e 2

　　式中： d 10为等效粒径； e 为孔隙比，e=。暂取浆液扩散范围 D 内的渗透系数 K =5×10 -2 cm · s -1 ，具体需要根据土体有关性质而定。以下分别讨论在不同注浆压力和不同注浆时间条件下，浆液的扩散半径及浆液对管片产生的压力的变化情况。
4.1 不同注浆压力
　　当注浆时间 t= 30 min ，注浆压力分别取 0.1 ～0.9 MPa 时，将各参数代入式（ 5 ），进而将由式（ 5 ）得到的浆液扩散半径代入式（ 8 ），可得盾尾注浆时，浆液扩散半径、对管片产生的压力及单位面积的压力等如表 2 所示。

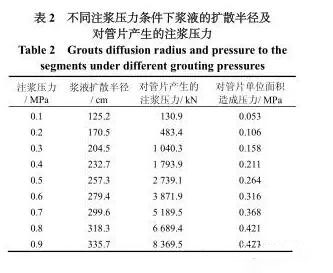
　　依据表 2 ，可绘出在注浆时间为 30 min 时，浆液扩散半径、对管片产生的压力及单位面积的压力等与注浆压力间的关系曲线。分别如图 5 ～ 7 所示。

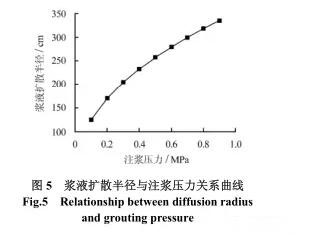
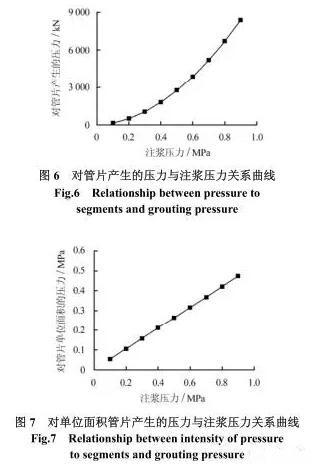
　　由曲线图可以看出，在相同注浆时间时，浆液扩散半径及对管片产生的压力均随注浆压力的增大而增大，且对管片产生的压力的增长速率大于浆液扩散半径的增长速率；对管片单位面积产生的压力也随注浆压力的增长而增长，呈现近似的线性关系。
　　可见，注浆压力的选择是需要慎重的，过大的注浆压力在增大浆液扩散范围、改善注浆加固效果的同时，增大了对管片本身的压力。依此类推，若注浆孔位于隧道顶部，也增大了对上覆土的压力，从而可能造成浆液外溢、地表隆起等现象。
4.2 不同注浆时间
　　仍按上述假定的已知条件，当注浆压力取0.3 MPa ，注浆时间分别取 10 ～ 90 min 时，将各参数代入式（ 5 ），进而将由式（ 5 ）得到的浆液扩散半径代入式（ 8 ），可得不同注浆时间条件下，采用盾尾注浆时，浆液扩散半径、对管片产生的压力及单位面积的压力等如表 3 所示。

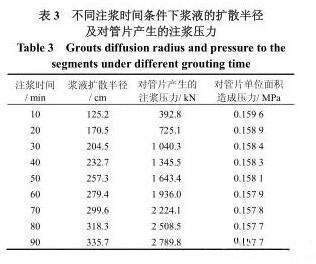
　　依据表 3 ，可绘出在注浆压力为 0.3 MPa 时，浆液扩散半径、对管片产生的压力及单位面积的压力等与注浆时间间的关系曲线，分别如图 8 ～ 10 所示。

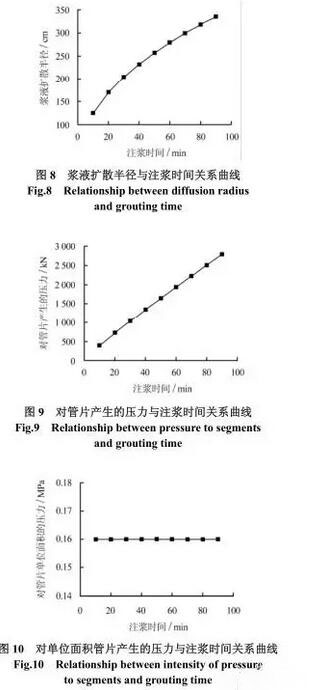
　　由曲线图可以看出，在相同注浆压力下，浆液扩散半径及对管片产生的压力均随注浆时间的增长而增加。相比之下，对管片产生的压力增长更快，其增长速度与注浆时间的增长速度近乎呈线性关系，对管片单位面积产生的压力基本保持不变。
　　可见，在盾构隧道壁后注浆施工中，注浆时间也是应该严格控制的，过长的注浆时间在增加了浆液的扩散范围(即增加了加固范围)的同时，也大大增加了对管片本身的荷载。
　　依据本文 3.2.2 中的分析，类似的结果在采用管片注浆时也可以得到，即浆液扩散半径及对管片的压力也随注浆压力和注浆时间的增长而增长，且对管片的压力将比采用盾尾注浆时大。
　　除注浆压力与注浆时间外，浆液的扩散半径还与土体特性（尤其是浆液扩散厚度范围内的渗透系数）、浆液特性（浆液黏度等）、建筑间隙厚度、注浆管半径等众多因素有关，本文不一一分析。
5 注浆压力的分布形式
　　依然采用本文第 4 节中的假设条件，并取注浆压力为 0.3 MPa，注浆时间为 30 min，则可由式（5）求得此时的浆液扩散半径r= 2.045 m，并可以依据式（6）求得各浆液扩散半径处管片受到的注浆压力大小，进而得到管片承受的注浆压力与浆液扩散半径间的关系曲线，如图 11 所示。

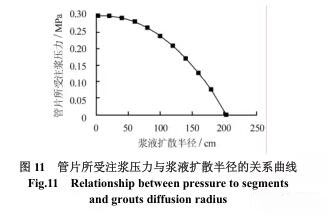
　　从图可以看出，盾构隧道壁后注浆施工过程中，对管片产生的注浆压力是呈抛物线形分布的，这与文献[3]中建议的注浆压力取三角形分布的结论是比较一致的。

6 结 论
　　在满足一定假设条件下，通过对盾尾注浆和管片注浆两种情况下的浆液渗透范围及因注浆而对管片造成的压力的理论及实例分析，得到了以下结论：
　　（1）盾构隧道壁后注浆会产生对管片的压力，该压力大小与注浆压力、注浆时间、浆液黏度、土体渗透率、建筑间隙厚度、注浆管半径等众多因素有关。
　　（2）盾尾间隙的存在相当于增大了一定范围内土体的孔隙率，进而大大增大了该范围内土体的渗透率，该孔隙率会对注浆效果及施工中产生的荷载造成重要影响。
　　（3）在相同土质和注浆参数下，管片注浆对管片产生的压力一般要大于盾尾注浆对管片产生的压力。随注浆浆液扩散半径的增大，对管片产生的压力也会随之增大。
　　（4）在一定土质和浆液性质条件下，改变注浆压力和注浆时间均可以改变注浆效果，调整浆液的扩散范围和对管片产生的压力，但改变速度有所差异。
　　（5）通过调整浆液本身的参数可以改变注浆效果，如改变浆液黏度等。